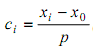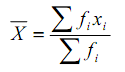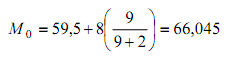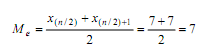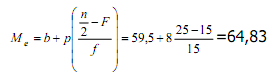Pengukuran Gejala Pusat (Mean, Modus, Median)
A. Pengertian Ukuran Gejala Pusat
Ukuran gejala pusat
adalah suatu ukuran yang digunakan untuk mengetahui kumpulan data
mengenai sampel atau populasi yang disajikan dalam tabel atau diagram.
1. Ukuran gejala pusat adalah suatu ukuran yang digunakan untuk mengetahui kumpulan data mengenai sampel atau populasi yang
disajikan dalam tabel dan diagram, yang dapat mewakili sampel atau populasi. Ada beberapa macam ukuran tendensi sentral, yaitu rata-rata (mean), median, modus, kuartil, desil dan persentil.
disajikan dalam tabel dan diagram, yang dapat mewakili sampel atau populasi. Ada beberapa macam ukuran tendensi sentral, yaitu rata-rata (mean), median, modus, kuartil, desil dan persentil.
2. Gejala pusat sebagai nilai rata-rata
yang mempunyai kecenderungan memusat, sehingga sering disebut ukuran
kecenderungan memusat (measures of central tendency). Beberapa jenis
rata-rata yang sering digunakan adalah rata-rata hitung (arithmetic mean
atau sering disingkat mean saja), lalu rata-rata ukur (geometric mean),
kemudian rata-rata harmonis (harmonic mean). Dan umumnya terdapat
istilah mean ,median, dan modus.
3. Gejala pusat pada hakekatnya
menganggap rata-rata (average) dapat merupakan nilai yang cukup
representatif bagi penggambaran nilai-nilai yang terdapat dalam data
yang bersangkutan. Rata-rata sedemikian itu dapat dianggap sebagai nilai
sentral dan dapat digunakan sebagai pengukuran lokasi sebuah distribusi
frekuensi. Statistik mengenal bermacam-macam rata-rata dengan nama-nama
yang khas, yaitu rata-rata hitung (mean), median, modus, rata-rata ukur
dan rata-rata harmonis itu semua merupakan jenis rata-rata yang lazim
digunakan sebagai pengukuran lokasi atau pengukuran tendensi sentral
(central tendency) dari sebuah distribusi.
B. Macam-macam Ukuran Gejala Pusat
MEAN
1. Rata-rata hitung / Mean
Dalam kegiatan penelitian, rata-rata(mean) mempunyai kedudukan yang penting dibandingkan ukuran gejala pusat lainnya. Hampir setiap kegiatan penelitian ilmiah selalu menggunakan rata-rata (mean).
Adapun cara untuk mencari mean dibedakan berdasarkan jenis penyajian data
a. Data tunggal dengan seluruh skornya berfrekuensi satu
Dalam kegiatan penelitian, rata-rata(mean) mempunyai kedudukan yang penting dibandingkan ukuran gejala pusat lainnya. Hampir setiap kegiatan penelitian ilmiah selalu menggunakan rata-rata (mean).
Adapun cara untuk mencari mean dibedakan berdasarkan jenis penyajian data
a. Data tunggal dengan seluruh skornya berfrekuensi satu
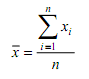
dimana xi = data ke-i dan n = jumlah data
Contoh :
Nilai Statistik dari 10 mahasiswa STMIK adalah sebagai berikut :
8 6 6 7 8 7 7 8 6 6
jadi meannya adalah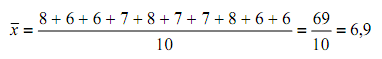
b. Data tunggal sebagian atau seluruh skornya berfrekuensi lebih dari satuNilai Statistik dari 10 mahasiswa STMIK adalah sebagai berikut :
8 6 6 7 8 7 7 8 6 6
jadi meannya adalah
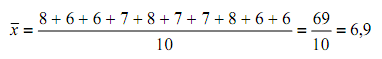

Maka
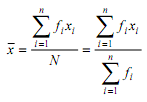
dengan xi merupakan nilai data
c. Data kelompok (dalam distribusi frekuensi)Cara mencari mean data kelompok ada dua , yaitu cara panjang dan cara pendek (sandi).
a) Cara panjang
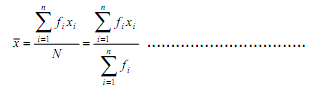
dengan xi merupakan tanda kelas dari interval ke-i
dan f merupakan frekuensi interval ke-i
b) Cara pendek / sandidan f merupakan frekuensi interval ke-i
Adapun langkah- langkanya adalah sebagai berikut :
1. Ambil sembarang tanda kelas ( biasanya yang letaknya ditengah) , misalnya x0
2. Hitung ci dengan rumus
3. Rumusan mean dengan cara pendek
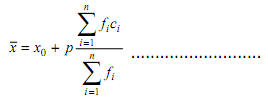
Contoh diperoleh rata-rata sebagai berikut :
a. Cara panjang
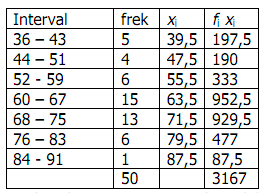
Berdasarkan persamaan pada cara panjang diperoleh rata-rata hitung dari data tersebut adalah
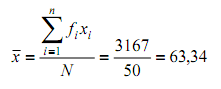
b. Cara pendek / sandi
Diambil x0 = 63,5 (tanda kelas ke-4) dan diketahui p = 8, maka diperoleh
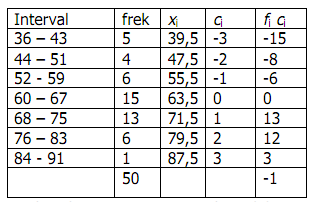
Berdasarkan persamaan pada cara pendek/sandi diperoleh rata- rata hitung
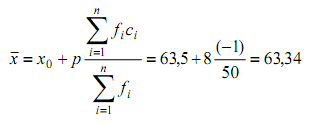
2. Rata-rata Tertimbang
Rata-rata tertimbang adalah rata-rata
yang memperhitungkan frekuensi dari tiap-tiap nilai variabel. Rumus
untuk rata-rata ini adalah :
Contoh :
Jika 5 mahasiswa mendapat nilai 70 : 6
mahasiswa mendapat 69 : 3 mahasiswa mendapat nilai 45 : 1 seorang
mahasiswa mendapat nilai 80 : 1 dan seorang lagi mendapat nilai 56 untuk
data tersebut sebaliknya ditulis sebagai berikut :
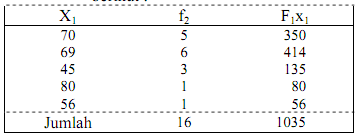
Pada nilai rata-rata ujian tersebut untuk ke-16 mahasiswa itu ialah :
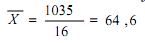
3. Rata-rata Gabungan
Rata-rata gabungan, yaitu rata-rata dari
beberapa sampel lalu disajikan satu. Rata-rata gabungan adalah cara yang
tepat untuk menggabungkan rata-rata hitung dari beberapa sampel.
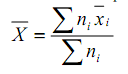
Contoh :
Tiga sub sampel masing-masing berukuran 10, 6, 8 dan rata-ratanya 145, 118, dan 162. Berapa rata-ratanya?
Jawab
MODUS (Mo)
Modus adalah nilai yang mempunyai frekuensi paling banyak. Modus tidak harus tunggal,artinya nilainya bisa lebih dari satu. Adapun cara mencari modus untuk data tunggal tinggal dilihat frekuensinya. Untuk data dalam daftar distribusi frekuensi, modus ditentukan dengan rumus :
Modus adalah nilai yang mempunyai frekuensi paling banyak. Modus tidak harus tunggal,artinya nilainya bisa lebih dari satu. Adapun cara mencari modus untuk data tunggal tinggal dilihat frekuensinya. Untuk data dalam daftar distribusi frekuensi, modus ditentukan dengan rumus :

dengan
b = batas bawah kelas modus yaitu kelas interval dengan frekuensi terbanyak
p = panjang interval kelas modus
b1 = frekuensi kelas modus dikurangi frekuensi kelas sebelum kelas modus
b2 = frekuensi kelas modus dikurangi frekuensi kelas sesudah kelas modus
Jika rumus di atas digunakan untuk mencari modus dari tabel di bawah ini

Maka diperoleh :
a. kelas modus = kelas ke-4
b. b = 59,5
c. b1 = 15 – 6 = 9
d. b2 = 15 – 13 = 2
e. p = 8
MEDIAN (Me)
Median adalah suatu nilai yang membagi distribusi data menjadi dua bagian yang sama besar atau suatu nilai yang menbagi 50% frekuensi bagian atas dan 50% frekuensi bagian bawah, sehingga frekuensi yang terdapat di atas sama dengan frekuensi yang trdapat di bawah. Oleh karena itu median dari sejumlah data tergantung pada frekuensinya bukan variasi nilai- nilainya.
Adapun cara mencari median, antara lain :
Median adalah suatu nilai yang membagi distribusi data menjadi dua bagian yang sama besar atau suatu nilai yang menbagi 50% frekuensi bagian atas dan 50% frekuensi bagian bawah, sehingga frekuensi yang terdapat di atas sama dengan frekuensi yang trdapat di bawah. Oleh karena itu median dari sejumlah data tergantung pada frekuensinya bukan variasi nilai- nilainya.
Adapun cara mencari median, antara lain :
a. Data tunggal sebagian atau seluluh skornya berfrekuensi lebih dari satu
Sebelum dihitung mediannya, data diurutkan lebih dulu dari data yang terkecil ke yang terbesar. Rumusan median untuk data tunggal dibedakan jadi dua, yaitu :
Sebelum dihitung mediannya, data diurutkan lebih dulu dari data yang terkecil ke yang terbesar. Rumusan median untuk data tunggal dibedakan jadi dua, yaitu :
Contoh
1. Untuk contoh tabel sebelumnya dengan data 8 6 6 7 8 7 7 8 6 6.
Setelah data diurutkan diperoleh 6 6 6 6 7 7 7 8 8 8. Jumlah data genap sehingga untuk mencari median digunakan rumus di atas dan diperoleh
2. Diketahui data sebagai berikut.1. Untuk contoh tabel sebelumnya dengan data 8 6 6 7 8 7 7 8 6 6.
Setelah data diurutkan diperoleh 6 6 6 6 7 7 7 8 8 8. Jumlah data genap sehingga untuk mencari median digunakan rumus di atas dan diperoleh
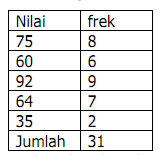
Tentukan median dari data di atas!
Untuk data di atas diketahui n ganjil, sehingga untuk mencari median digunakan rumus pertama dan diperoleh :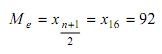
b. Data kelompok ( dalam distribusi frekuensi)
Untuk data yang disusun dalam daftar distribusi frekuensi, median dihitung dengan rumus :
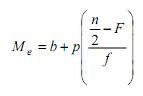
dengan
b = batas bawah kelas median
p = panjang kelas median
n = jumlah data
F = jumlah frekuensi kumulatif sebelum kelas median
f = frekuensi kelas median
Contoh
Dari tabel sebelumnya diperoleh kelas median terletak pada interval ke-4, sehingga diperoleh b = 59,5 ; p = 8; n = 50 ; F = 15 dan f = 15 akibatnya
C. Kelebihan dan Kekurangan Rata-rata, Median dan ModusDari tabel sebelumnya diperoleh kelas median terletak pada interval ke-4, sehingga diperoleh b = 59,5 ; p = 8; n = 50 ; F = 15 dan f = 15 akibatnya
Rata-rata
Kelebihan
- Rata-rata lebih populer dan lebih mudah digunakan.
- Dalam satu set data, rata-rata selalu ada dan hanya ada satu rata-rata.
- Dalam penghitungannya selalu mempertimbangkan semua nilai data.
- Tidak peka terhadap penambahan jumlah data.
- Variasinya paling stabil.
- Cocok digunakan untuk data yang homogen.
- Sangat peka terhadap data ekstrim. Jika data ekstrimnya banyak, rata-rata menjadi kurang mewakili (representatif).
- Tidak dapat digunakan untuk data kualitatif.
- Tidak cocok untuk data heterogen.
Kelebihan
- Tidak dipengaruhi oleh data ekstrim.
- Dapat digunakan untuk data kualitatif maupun kuantitatif.
- Cocok untuk data heterogen.
- Tidak mempertimbangkan semua nilai data.
- Kurang menggambarkan rata-rata populasi.
- Peka terhadap penambahan jumlah data.
Kelebihan
- Tidak dipengaruhi oleh data ekstrim.
- Cocok digunakan untuk data kuantitatif maupun kualitatif.
- Modus tidak selalu ada dalam satu set data.
- Kadang dalam satu set data terdapat dua atau lebih modus. Jika hal itu terjadi modus menjadi sulit digunakan.
- Kurang mempertimbangkan semua nilai.
- Peka terhadap penambahan jumlah data.
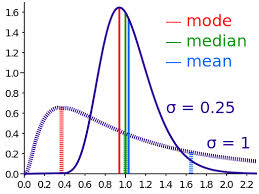
- Jika rata-rata, median dan modus memiliki nilai yang sama, maka nilai rata-rata, median dan modus akan terletak pada satu titik dalam kurva distribusi frekuensi. Kurva distribusi frekuensi tersebut akan terbentuk simetris.
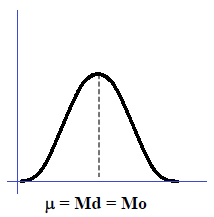
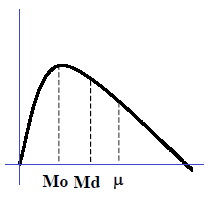
- Jika rata-rata lebih besar dari median, dan median lebih besar dari modus, maka pada kurva distribusi frekuensi, nilai rata-rata akan terletak di sebelah kanan, sedangkan median terletak di tengahnya dan modus di sebelah kiri. Kurva distribusi frekuensi akan terbentuk menceng ke kiri.
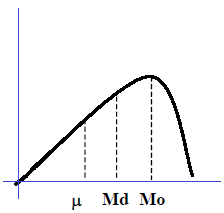
- Jika rata-rata lebih kecil dari median, dan median lebih kecil dari modus, maka pada kurva distribusi frekuensi, nilai rata-rata akan terletak di sebelah kiri, sedangkan median terletak di tengahnya dan modus di sebelah kanan. Kurva distribusi frekuensi akan terbentuk menceng ke kanan.
- Jika kurva distribusi frekuensi tidak simetris (menceng ke kiri atau ke kanan), maka biasanya akan berlaku hubungan antara rata-rata median dan modus sebagai berikut. Rata-rata – Modus = 3 (Rata-rata – Median)
Daftar Pustaka :
Suharyadi, & Purwanto. (2009). In Statistika untuk Ekonomi dan Keuangan Modern. Jakarta: Salemba Empat.Sudjana. (1991). In Statistika. Bandung: Tarsito.